dy和Δy之间的主要区别是什么?
全部展开
dy与Δy之差如下。1.表达的含义不同。
1,dy表示分化。
如果在点x处自变量的变化Δx与对应于函数Δy= A×Δx+ο(Δx)的变化Δy有关,则假定函数y = f(x)。在A不依赖于Δx的情况下,函数f(x)可被点x整除,AΔx是点x处的函数f(x)的导数,表示为dy,并且dy = A×Δx其中x = x0和dy,x = x0。
2.Δy表示函数的增量。
在点x处自变量的变化Δx与对应于函数Δy= A×Δx+ο(Δx)2的变化Δy有关。计算公式不同。
1,dy = f(x)dx。
如果该函数是可分的,则Δy=AΔx+ a(x),其中A是常数,而a(x)是Δx-0,则它是一个比Δx大的无穷大,并且dy =AΔx= Adx。
2.Δy= f(x +Δx)-f(x)。
函数Δy= f(x +Δx)-f(x)的增加可以表示为Δy=AΔx+或(Δx)。
第三,两者通常不相同,但可以通过数学公式转换。
1.通常,dy≠yy。
当Δx接近无限时间时,Dy等于Δy。
2.如果不同,则Δy= dy + o(Δx)。
O(Δx)无限小于Δx。
资料来源:百度百科-微分百度百科-微
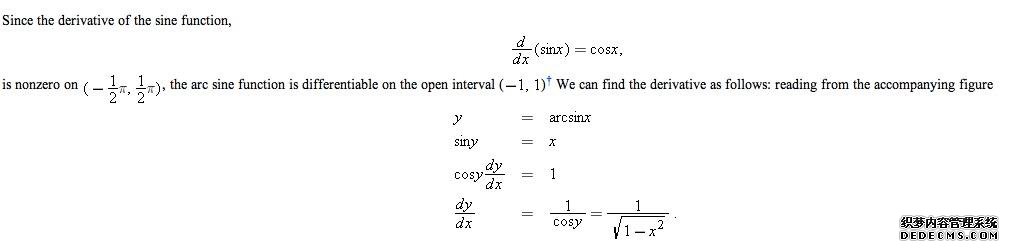
dy与Δy之差如下。1.表达的含义不同。
1,dy表示分化。
如果在点x处自变量的变化Δx与对应于函数Δy= A×Δx+ο(Δx)的变化Δy有关,则假定函数y = f(x)。在A不依赖于Δx的情况下,函数f(x)可被点x整除,AΔx是点x处的函数f(x)的导数,表示为dy,并且dy = A×Δx其中x = x0和dy,x = x0。
2.Δy表示函数的增量。
在点x处自变量的变化Δx与对应于函数Δy= A×Δx+ο(Δx)2的变化Δy有关。计算公式不同。
1,dy = f(x)dx。
如果该函数是可分的,则Δy=AΔx+ a(x),其中A是常数,而a(x)是Δx-0,则它是一个比Δx大的无穷大,并且dy =AΔx= Adx。
2.Δy= f(x +Δx)-f(x)。
函数Δy= f(x +Δx)-f(x)的增加可以表示为Δy=AΔx+或(Δx)。
第三,两者通常不相同,但可以通过数学公式转换。
1.通常,dy≠yy。
当Δx接近无限时间时,Dy等于Δy。
2.如果不同,则Δy= dy + o(Δx)。
O(Δx)无限小于Δx。
资料来源:百度百科-微分百度百科-微
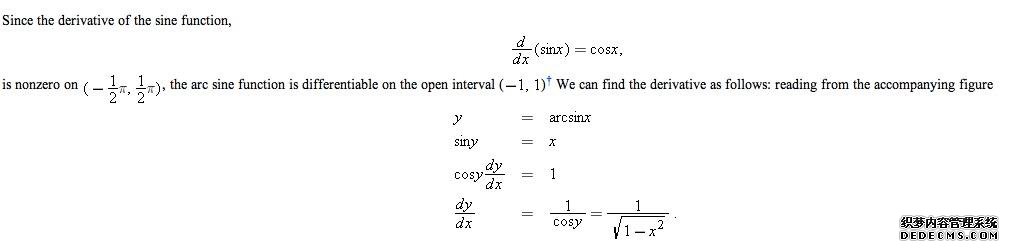
上一篇:参见UL杆+水滴轮。
下一篇:没有了